二叉树后序遍历（递归与非递归）算法C语言实现

1年前 (2024-04-27)

二叉树后序遍历的实现思想是：从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。

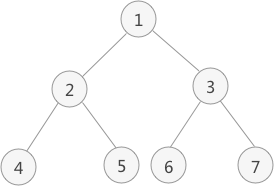
图 1 二叉树

如图 1 中，对此二叉树进行后序遍历的操作过程为：

从根节点 1 开始，遍历该节点的左子树（以节点 2 为根节点）；

遍历节点 2 的左子树（以节点 4 为根节点）；

由于节点 4 既没有左子树，也没有右子树，此时访问该节点中的元素 4，并回退到节点 2 ，遍历节点 2 的右子树（以 5 为根节点）；

由于节点 5 无左右子树，因此可以访问节点 5 ，并且此时节点 2 的左右子树也遍历完成，因此也可以访问节点 2；

此时回退到节点 1 ，开始遍历节点 1 的右子树（以节点 3 为根节点）；

遍历节点 3 的左子树（以节点 6 为根节点）；

由于节点 6 无左右子树，因此访问节点 6，并回退到节点 3，开始遍历节点 3 的右子树（以节点 7 为根节点）；

由于节点 7 无左右子树，因此访问节点 7，并且节点 3 的左右子树也遍历完成，可以访问节点 3；节点 1 的左右子树也遍历完成，可以访问节点 1；

到此，整棵树的遍历结束。

由此，对图 1 中二叉树进行后序遍历的结果为：

4 5 2 6 7 3 1

递归实现

后序遍历的递归实现代码为：

#include <stdio.h>
#include <string.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//初始化树的函数
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
//模拟操作结点元素的函数，输出结点本身的数值
void displayElem(BiTNode* elem){
printf("%d ",elem->data);
}
//后序遍历
void PostOrderTraverse(BiTree T){
if (T) {
PostOrderTraverse(T->lchild);//遍历左孩子
PostOrderTraverse(T->rchild);//遍历右孩子
displayElem(T);//调用操作结点数据的函数方法
}
//如果结点为空，返回上一层
return;
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
printf("后序遍历: \n");
PostOrderTraverse(Tree);
}

运行结果：

后序遍历:

4 5 2 6 7 3 1

非递归实现

递归算法底层的实现使用的是栈存储结构，所以可以直接使用栈写出相应的非递归算法。

后序遍历是在遍历完当前结点的左右孩子之后，才调用操作函数，所以需要在操作结点进栈时，为每个结点配备一个标志位。当遍历该结点的左孩子时，设置当前结点的标志位为 0，进栈；当要遍历该结点的右孩子时，设置当前结点的标志位为 1，进栈。

这样，当遍历完成，该结点弹栈时，查看该结点的标志位的值：如果是 0，表示该结点的右孩子还没有遍历；反之如果是 1，说明该结点的左右孩子都遍历完成，可以调用操作函数。

完整实现代码为：

#include <stdio.h>
#include <string.h>
#define TElemType int
int top=-1;//top变量时刻表示栈顶元素所在位置
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//初始化树的函数
void CreateBiTree(BiTree *T){
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=1;
(*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->data=2;
(*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->lchild->rchild->data=5;
(*T)->lchild->rchild->lchild=NULL;
(*T)->lchild->rchild->rchild=NULL;
(*T)->rchild->data=3;
(*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->lchild->data=6;
(*T)->rchild->lchild->lchild=NULL;
(*T)->rchild->lchild->rchild=NULL;
(*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->rchild->rchild->data=7;
(*T)->rchild->rchild->lchild=NULL;
(*T)->rchild->rchild->rchild=NULL;
(*T)->lchild->lchild->data=4;
(*T)->lchild->lchild->lchild=NULL;
(*T)->lchild->lchild->rchild=NULL;
}
//弹栈函数
void pop( ){
if (top==-1) {
return ;
}
top--;
}
//模拟操作结点元素的函数，输出结点本身的数值
void displayElem(BiTNode* elem){
printf("%d ",elem->data);
}
//后序遍历非递归算法
typedef struct SNode{
BiTree p;
int tag;
}SNode;
//后序遍历使用的进栈函数
void postpush(SNode *a,SNode sdata){
a[++top]=sdata;
}
//后序遍历函数
void PostOrderTraverse(BiTree Tree){
SNode a[20];//定义一个顺序栈
BiTNode * p;//临时指针
int tag;
SNode sdata;
p=Tree;
while (p||top!=-1) {
while (p) {
//为该结点入栈做准备
sdata.p=p;
sdata.tag=0;//由于遍历是左孩子，设置标志位为0
postpush(a, sdata);//压栈
p=p->lchild;//以该结点为根结点，遍历左孩子
}
sdata=a[top];//取栈顶元素
pop();//栈顶元素弹栈
p=sdata.p;
tag=sdata.tag;
//如果tag==0，说明该结点还没有遍历它的右孩子
if (tag==0) {
sdata.p=p;
sdata.tag=1;
postpush(a, sdata);//更改该结点的标志位，重新压栈
p=p->rchild;//以该结点的右孩子为根结点，重复循环
}
//如果取出来的栈顶元素的tag==1，说明此结点左右子树都遍历完了，可以调用操作函数了
else{
displayElem(p);
p=NULL;
}
}
}
int main(){
BiTree Tree;
CreateBiTree(&Tree);
printf("后序遍历: \n");
PostOrderTraverse(Tree);
}

运行结果

后序遍历:

4 5 2 6 7 3 1